Pertemuan ke 4 - Tree - 2101662032 - Arya Surya Sabara Cia

TREE

  1. PENGERTIAN TREE
    Kumpulan node yang saling terhubung satu sama lain dalam suatu kesatuan yang membentuk layakya struktur sebuah pohon. Struktur pohon adalah suatu cara merepresentasikan suatu struktur hirarki (one-to-many) secara grafis yang mirip sebuah pohon, walaupun pohon tersebut  hanya tampak sebagai kumpulan node-node  dari atas ke bawah. Suatu struktur data yang tidak linier yang menggambarkan  hubungan yang hirarkis (one-to-many) dan tidak linier antara elemen-elemennya.
    Sebuah binary search tree (bst) adalah sebuah pohon biner yang boleh kosong, dan setiap nodenya harus memiliki identifier/value. Value pada semua node subpohon sebelah kiiri adalah selalu lebih kecil dari value dari root, sedangkan value subpohon di sebelah kanan adalah sama atau lebih besar dari value pada root, masing-masing subpohon tersebut (kiri dan kanan) itu sendiri adalah juga binary search tree.
    Struktur data bst sangat penting dalam struktur pencarian, misalkan dalam kasus pencarian dalam sebuah list, jika list sudah dalam keadaan terurut maka proses pencarian akan semakin cepat, jika kita menggunakan  list contigue(linked list) dan melakukan pencarian biner,akan tetapi  jika kita ingin melakukan perubahan isi list (insert atau delete), menggunakan list contigue akan sangat lambat, karena prose insert dan delete dalam list contigue butuh memindahkan linked-list, yang untuk operasi insert atau delete tinggal mengatur- atur pointer,akan tetapi pada n-linked list, kita tidak bisa melakukan pointer sembarangan setiap saat, kecuali hanya satu kali dengan kata lain hanya secara sequential.
  2. DEKLARASI TREE
    Jika kita memperhatikan setiap simpul dalam pohon biner, kita bisa menyusun  struktur data yang tepat dari simpul-simpul tersebut. Kita dapat melihat bahwa dalam  setiap simpul selalu berisi dua buah pointer untuk menunjuk ke cabang kiri dan cabang  kanan, dan informasi yang akan disimpan dalamsimpul tersebut. Dengan memperhatikan hal ini, simpul dalam pohon biner disajikan sebagai berikut:
    3. Gambar
    Sesuai dengan gambar 7.1, maka deklarasi list yang sesuai adalah:
    typedef char TypeInfo;
    typedef struct Simpul *Tree;
    struct Simpul {
    TypeInfo Info;
    tree Kiri, /* cabang kiri */
    Kanan; /* cabang kanan */
    };
  3. ISTILAH DALAM TREE
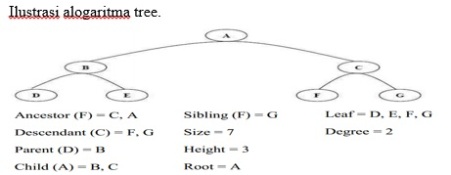
    Gambar
    Gambar


  4. JENIS-JENIS TREE
    BINARY TREE
    Tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal dua sub pohon dan kedua subpohon harus terpisah.

    Kelebihan struktur Binary Tree :
  • Mudah dalam penyusunan algoritma sorting
  • Searching data relatif cepat
  • Fleksibel dalam penambahan dan penghapusan data
Gambar

Gambar

Gambar

  1. KUNJUNGAN PADA POHON BINER
Sebuah pohon biner memiliki operasi  traversal  yaitu suatu kunjungan pada
suatu simpul tepat satu kali. Dengan melakukan kunjungan lengkap kita akan
memperoleh urutan informasi secara linier yang tersinpan di dalam pohon biner.
Terdapat tiga jenis kunjungan pada pohon biner, yaitu :
  1. PREORDER
Kunjungan jenis ini mempunyai urutan kunjungan sebagai berikut :
–  Cetak isi simpul yang dikunjungi.
–  Kunjungi cabang kiri.
–  Kunjungi cabang kanan.
Prosedur untuk melakukan traversal secara PREORDER adalah sebagai berikut:
Gambar

  1. INORDER
Kunjungan jenis ini mempunyai urutan kunjungan sebagai berikut :
–  Kunjungi cabang kiri.
–  Cetak isi simpul yang dikunjungi.
–  Kunjungi cabang kanan.
Prosedur untuk melakukan traversal secara INORDER adalah sebagai berikut:
Gambar

  1. POSTORDER
Kunjungan jenis ini mempunyai urutan kunjungan sebagai berikut :
–  Kunjungi cabang kiri.
–  Kunjungi cabang kanan.
–  Cetak isi simpul yang dikunjungi
BERIKUT MERUPAKN CONTOH PROGRAMNYA
#include<stdio.h>//header file
#include<conio.h>
/* Deklarasi struct */
typedef struct Node{
      int data;    //data pada tree
      Node *kiri;  //penunjuk node anak kiri
      Node *kanan; //penunjuk node anak kanan
};
/* Fungsi untuk memasukkan data ke dalam tree */
void tambah(Node **root, int databaru){
      if((*root) == NULL){       //jika pohon/subpohon masih kosong
            Node *baru;//node “baru” dibentuk…
            baru = new Node;//berdasarkan struct “Node”
            baru->data = databaru; //data node baru diisi oleh variabel databaru
            baru->kiri = NULL;//penunjuk kiri node baru masih kosong
            baru->kanan = NULL;//penunjuk kanan node baru masih kosong
            (*root) = baru; //node pohon (root) diletakkan pada node baru
            (*root)->kiri = NULL;//penunjuk kiri node root masih kosong
            (*root)->kanan = NULL; //penunjuk kanan node root masih kosong
            printf(“Data bertambah!”);
      }
      else if(databaru < (*root)->data)//jika databaru kurang dari data node root…
            tambah(&(*root)->kiri, databaru);//tambahkan databaru pada subpohon kiri
      else if(databaru > (*root)->data)//jika databaru lebih dari data node root…
            tambah(&(*root)->kanan, databaru); //tambahkan databaru pada subpohon kanan
      else if(databaru == (*root)->data)//jika databaru sama dengan data node root
            printf(“Data sudah ada!”);//databaru tidak dapat ditambahkan pada tree
}
/* Fungsi untuk menampilkan data secara pre-order
   (data ditampilkan dari node induk, node anak kiri, lalu node anak kanan)
*/
void preOrder(Node *root){ 
      if(root != NULL){//jika pohon/subpohon tidak kosong
            printf(“%d “, root->data);//menampilkan data node yang dikunjungi
      preOrder(root->kiri);//mengunjungi node anak kiri
      preOrder(root->kanan); //mengunjungi node anak kanan
      }
}
/* Fungsi untuk menampilkan data secara in-order
   (data ditampilkan dari node anak kiri, node induk, lalu node anak kanan)
*/
void inOrder(Node *root){
      if(root != NULL){//jika pohon/subpohon tidak kosong…
      inOrder(root->kiri);//mengunjungi node anak kiri
      printf(“%d “, root->data);//menampilkan data node yang dikunjungi
      inOrder(root->kanan);//mengunjungi node anak kanan
      }
}
              
/* Fungsi untuk menampilkan data secara post-order
   (data ditampilkan dari node anak kiri, node anak kanan, lalu node induk)
*/
void postOrder(Node *root){
     if(root != NULL){//jika pohon/subpohon tidak kosong
     postOrder(root->kiri); //mengunjungi node anak kiri
     postOrder(root->kanan);//mengunjungi node anak kanan
     printf(“%d “, root->data); //menampilkan data node yang dikunjungi
     }
}
main(){
     int pil, c;
     Node *pohon, *t;
     pohon = NULL;
     do{
           int data;
           printf(“MENU\n”);
           printf(“1. Tambah\n”);
           printf(“2. Lihat Pre-Order\n”);
           printf(“3. Lihat In-Order\n”);
           printf(“4. Lihat Post-Order\n”);
           printf(“5. Exit\n”);
           printf(“Pilihan : “); scanf(“%d”, &pil);
           switch(pil){
           case 1 :
                printf(“Data baru : “);
                scanf(“%d”, &data);
                tambah(&pohon, data);
                break;
           case 2 :
                if(pohon != NULL)
                     preOrder(pohon);
                else
                     printf(“Masih kosong!”);
                break;
           case 3 :
                if(pohon != NULL)
                     inOrder(pohon);
                else
                      printf(“Masih kosong!”);
                break;
           case 4 :
                if(pohon != NULL)
                     postOrder(pohon);
                else
                     printf(“Masih kosong!”);
                break;
           }
           getch();
           printf(“\n”);
     }
     while(pil != 5);
}
HASIL
Gambar

Gambar

          Aplikasi pohon Biner
Notasi Prefix, Infix dan Postfix
Pada bagian ini akan dibahas tentang bagaimana menyusun sebuah Pohon Binar yang apabila dikunjungisecara PreOrder akan menghasilkan Notasi Prefix,kunjungan secara InOrder menghasilkan Notasi Infix, dankunjungan PostOrder menghasilkan Notasi Postfix.

Contoh kasus dan Program
·         Contoh Program Tree dalam C++
#include <iostream.h>
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
struct Node{
int data;
Node *kiri;
Node *kanan;
};
int count;
void tambah(Node **root, int databaru)
{
if((*root) == NULL){
Node *baru;
baru = new Node;
baru->data = databaru;
baru->kiri = NULL;
baru->kanan = NULL;
(*root) = baru;
(*root)->kiri = NULL;
(*root)->kanan = NULL;
printf("Data telah Dimasukkan");
}
else if(databaru < (*root)->data)
tambah(&(*root)->kiri,databaru);
else if(databaru > (*root)->data)
tambah(&(*root)->kanan,databaru);
else if(databaru == (*root)->data)
printf("Data sudah ada!!");
}
void preOrder(Node *root){
if(root != NULL){
printf("%d " ,root->data);
preOrder(root->kiri);
preOrder(root->kanan);
}
}
void inOrder(Node *root){
if(root != NULL){
inOrder(root->kiri);
printf("%d ",root->data);
inOrder(root->kanan);
}
}
void postOrder(Node *root){
if(root != NULL){
postOrder(root->kiri);
postOrder(root->kanan);
printf("%d ",root->data);
}
}
void search(Node **root, int cari)
{
if((*root) == NULL){
printf("Maaf,Data tidak ditemukan!");
}
else if(cari < (*root)->data)
search(&(*root)->kiri,cari);
else if(cari > (*root)->data)
search(&(*root)->kanan,cari);
else if(cari == (*root)->data)
printf("Data ditemukan!!!");
}
void hapus(Node **root, int del)
{
if((*root) == NULL){
printf("Data tidak ada!!");
}
else if(del < (*root)->data)
hapus(&(*root)->kiri,del);
else if(del > (*root)->data)
hapus(&(*root)->kanan,del);
else if(del == (*root)->data)
{
(*root)=NULL;
printf("Data telah Terhapus");
}
}
int main(){
int pil,cari,del;
Node *pohon;
pohon = NULL;
do{
int data;
system("cls");
printf("       PROGRAM TREE LANJUTAN    \n");
printf("================================\n");
printf("   1. Masukkan Data             \n");
printf("   2. Transverse                \n");
printf("   3. Cari                      \n");
printf("   4. Hapus                     \n");
printf("   5. Clear Data                \n");
printf("   6. Keluar                    \n");
printf("================================\n");
printf("Masukkan Pilihan Anda : ");
scanf("%d",&pil);
switch(pil){
case 1:
printf("Masukkan data baru : ");
scanf("%d", &data);
tambah(&pohon,data);
break;
case 2:
printf("\nPreOrder : ");
if(pohon!=NULL) preOrder(pohon);
else printf("Data masih kosong");
printf("\ninOrder : ");
if(pohon!=NULL) inOrder(pohon);
else printf("Data masih kosong");
printf("\npostOrder : ");
if(pohon!=NULL) postOrder(pohon);
else printf("Data masih kosong");
break;
case 3:
printf("Cari data : ");
scanf("%d", &cari);
search(&pohon,cari);
break;
case 4:
printf("Hapus data : ");
scanf("%d", &del);
hapus(&pohon,del);
break;
case 5:
pohon = NULL;
printf("Semua data telah terhapus");
break;
case 6:
return 0;
default:
printf("Maaf, pilihan Anda Salah");
}
getch();
}while(pil!=7);
}
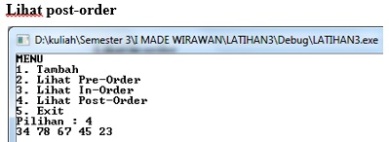
Tampilan program saat dijalankan :

Tampilan Transverse setelah diinput data 1,3,7 dan 5.



2101662032 - ARYA SURYA SABARA CIA

Komentar

Posting Komentar

Postingan populer dari blog ini

Pertemuan ke 5 - Binary Search Tree - 2101662032 - Arya Surya Sabara Cia

Gambar
BINARY SEARCH TREE PENGERTIAN BINARY TREE Binary Tree adalah struktur data yang hampir mirip dengan linked list untuk menyimpan koleksi dari data. Linked list dapat dianalogikan sebagai rantai linear sedangkan Binary tree bisa digambarkan sebagai rantai tidak linear, binary tree dikelompokkan menjadi unordered binary tree dan ordered binary tree. Binary Search Tree adalah tree yang terurut. ada beberapa aturan yang perlu diperhatikan saat membuat sebuah BST,yaitu: 1. Semua data dibagian kiri sub-tree dari node A selalu lebih kecil dari data dalam node A itu sendiri. 2. Semua data dibagian kanan sub-tree dari node A selalu lebih besar atau sama dengan data dari dalam node A itu. PEMBENTUKAN BST Bila diketahui sederetan data 5, 3, 7, 1, 4, 6, 8, 9 maka proses inserting (memasukkan) data tersebut dalam algoritma BST langkah per langkah adalah sebagai berikut. Langkah 1: Pemasukan data 5 sebagai root( akar) Langkah 2: Pemasukan data 3 disebelah kiri simpul 5 karena 3 < 5....
Baca selengkapnya